Tablesample In PostgreSQL 9.5
PostgreSQL 9.5 introduces support for TABLESAMPLE, an SQL SELECT clause that returns a random sample from a table.
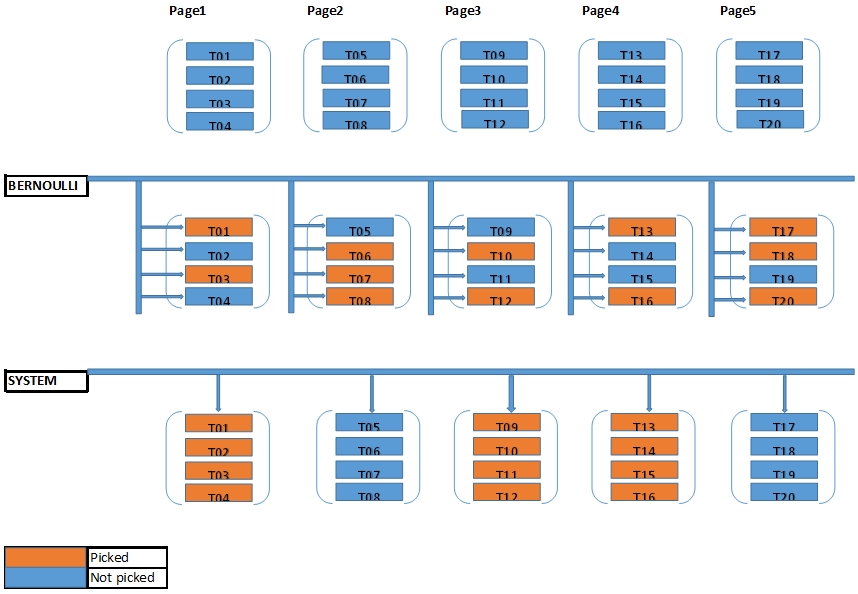
SQL:2003 defines two sampling methods: SYSTEM and BERNOULLI.
The SYSTEM method uses random IO whereas BERNOULLI uses sequential IO. SYSTEM is faster, but BERNOULLI gives us a much better random distribution because each tuple (row) has the same probability on being selected.
The SYSTEM sampling method does block/page level sampling; it reads and returns random pages from disk. Thus it provides randomness at the page level instead of the tuple level. The BERNOULLI sampling method does a sequential scan on the whole table and picks tuples randomly.
SYNTAX
The TABLESAMPLE clause was defined in the SQL:2003 standard. The SYNTAX implemented by PostgreSQL 9.5 is as follows:
SELECT select_expression
FROM table_name
TABLESAMPLE sampling_method ( argument [, ...] ) [ REPEATABLE ( seed ) ]
...
Although it cannot be used for UPDATE or DELETE queries, it can be used with any join query and aggregation.
PostgreSQL supports both sampling methods required by the standard, but the implementation allows for custom sampling methods to be installed as extensions.
Both SYSTEM and BERNOULLI take as an argument the percentage of rows in table_name that are to be returned.
If table_name has N rows and the requested percentage (a floating point value between 0 and 100) is S then:
SYSTEMpicks (N * S/100) pages where each page is selected with S/100 probability.BERNOULLIpicks (N * S/100) rows where each row is selected with S/100 probability.
SYSTEM returns all rows in each selected page, but the number of rows per page depends on the size of each row. That’s why we cannot guarantee that the provided percentage will result in the expected number of rows.
Let’s suppose we have a table called ts_test with 10 million rows. We can find the number of pages this table occupies using the following SQL:
SELECT relpages FROM pg_class WHERE relname = 'ts_test';
And the output will be similar to:
relpages
----------
93457
(1 row)
So if 10 million rows are stored in 93457 pages then a single page may be expected to store 10 000 000 / 93 457 = 107 rows.
In order to retrieve approximately 1000 rows, we need to request 1000 * 100 / 10 000 000 = 0.01% of the table’s rows.
But note that every page may not be filled with as many live tuples as it can hold. If you have recently deleted a large number of rows, you will need to run VACUUM FULL to reclaim the unused space and reduce the total relpages used by the table.
On the other hand, the BERNOULLI method works at the row level, so it has a better chance of returning a percentage close to the requested percentage.
The seed parameter to the optional REPEATABLE clause allows us to define a random seed for the sampling process. Given the same seed, PostgreSQL normally returns the same result set. However it may return different rows on certain conditions where the distribution of tuples among pages changes.
One important thing to consider is that any conditionals in the WHERE clause will be applied after the sampling. Which means that the requested number of rows will be picked first and then be filtered using the conditionals expressed in the WHERE clause.
Examples
Let’s create a simple table with two columns:
CREATE TABLE ts_test (
id SERIAL PRIMARY KEY,
title TEXT
);
And insert 1M rows into it:
INSERT INTO ts_test (title)
SELECT
'Record #' || i
FROM
generate_series(1, 1000000) i;
SYSTEM Table Sampling
In this example our aim is to retrieve the same number of samples as the table gets bigger in each test. We will be observing the amount of increase in the time it takes to retrieve 1000 samples with the SYSTEM sampling method.
The SQL template for this method is like the following:
SELECT * FROM ts_test TABLESAMPLE SYSTEM(percentage)
The percentage parameter will be updated as the number of rows in the ts_test table increases.
For 10000 rows, 1000 samples means that we should pick 10% of the table. This is what the resulting plan looks like:
tablesample_test=# explain analyze select * from ts_test tablesample system(10);
QUERY PLAN
---------------------------------------------------------------------------------------------------------------------
Sample Scan (system) on ts_test (cost=0.00..34.00 rows=1000 width=16) (actual time=0.022..0.230 rows=1127 loops=1)
Planning time: 131.779 ms
Execution time: 0.317 ms
(3 rows)
The planner uses a sample scan node for this query, and PostgreSQL returns 1127 rows (rather than the expected 1000) for these specific set of picked pages. Subsequent executions may return a slightly different number of samples as well.
The execution time is observed as 0.317 ms.
For 1 000 000 rows, the percentage is 0.1% this time.
tablesample_test=# explain analyze select * from ts_test tablesample system(0.1);
QUERY PLAN
---------------------------------------------------------------------------------------------------------------------
Sample Scan (system) on ts_test (cost=0.00..34.00 rows=1000 width=18) (actual time=0.033..0.296 rows=1099 loops=1)
Planning time: 15.186 ms
Execution time: 0.377 ms
(3 rows)
The execution time seems to be marginally increased.
Finally, for 10 000 000 rows the EXPLAIN statement shows the following:
tablesample_test=# explain analyze select * from ts_test tablesample system(0.01);
QUERY PLAN
---------------------------------------------------------------------------------------------------------------------
Sample Scan (system) on ts_test (cost=0.00..34.00 rows=1000 width=18) (actual time=0.115..0.914 rows=1099 loops=1)
Planning time: 0.195 ms
Execution time: 0.995 ms
(3 rows)
The time cost seems to be the triple of 1 000 000 row-table. However, considering a table with 10 million rows, this increase in execution time may be acceptable for a range of scenarios.
BERNOULLI Table Sampling
In this example, we have a similar goal but this time we will be using the BERNOULLI sampling method.
The SQL template for this is similar as well:
SELECT * FROM ts_test TABLESAMPLE BERNOULLI(percentage)
For 10% of a 10 000 row table:
tablesample_test=# explain analyze select * from ts_test tablesample bernoulli(10);
QUERY PLAN
------------------------------------------------------------------------------------------------------------------------
Sample Scan (bernoulli) on ts_test (cost=0.00..73.00 rows=1000 width=16) (actual time=0.006..0.758 rows=1003 loops=1)
Planning time: 0.151 ms
Execution time: 0.820 ms
(3 rows)
Compared to SYSTEM‘s 1127, returned sample count 1003 is much closer to 1000. This reflects results of BERNOULLI‘s sequential scanning characteristics.
Also the execution time is more than doubled. This also reflects the performance difference between BERNOULLI‘s sequential IO and SYSTEM‘s random IO.
For 1 000 000 rows, EXPLAIN reveals a significant increase in the execution time:
tablesample_test=# explain analyze select * from ts_test tablesample bernoulli(0.1);
QUERY PLAN
---------------------------------------------------------------------------------------------------------------------------
Sample Scan (bernoulli) on ts_test (cost=0.00..6378.00 rows=1000 width=16) (actual time=0.055..78.135 rows=1042 loops=1)
Planning time: 0.152 ms
Execution time: 78.219 ms
(3 rows)
A 100 times increase in the row count resulted in a 95 times increase in the execution time.
We can also observe this behavior for 10M rows:
tablesample_test=# explain analyze select * from ts_test tablesample bernoulli(0.01);
QUERY PLAN
----------------------------------------------------------------------------------------------------------------------------
Sample Scan (bernoulli) on ts_test (cost=0.00..63702.00 rows=1000 width=19) (actual time=0.707..779.128 rows=998 loops=1)
Planning time: 0.094 ms
Execution time: 779.244 ms
(3 rows)
Both the row count and execution time increased 10 times. Based on these 3 examples, we may say that there may be a linear correlation between the number of rows and the time it takes to sampling.
Repeatable Example
To demonstrate how REPEATABLE works, first we will choose a simple seed parameter. Supposing that we selected 200 as the seed to the random number generator:
SELECT * FROM ts_test TABLESAMPLE SYSTEM (0.001) REPEATABLE (200);
The query above gives us a sample distribution similar to the following:
| id | title |
| 741 | Record #741 |
| 742 | Record #742 |
| 743 | Record #743 |
| … | … |
Now suppose that no writes were done on ts_table during this period. Let’s run the exact query for the second time.
SELECT * FROM ts_test TABLESAMPLE SYSTEM (0.001) REPEATABLE (200);
The result set will be the same as above because the given seed, 200, was kept the same.
| id | title |
| 741 | Record #741 |
| 742 | Record #742 |
| 743 | Record #743 |
| … | … |
However, providing a different seed most likely will produce a quite different result set.
SELECT * FROM ts_test TABLESAMPLE SYSTEM (0.001) REPEATABLE (9000);
| id | title |
| 556 | Record #556 |
| 557 | Record #557 |
| 558 | Record #558 |
| … | … |
Extensibility
The TABLESAMPLE implementation can be extended with custom sampling methods. PostgreSQL 9.5 has an API for sampling functions, and includes two extensions: tsm_system_rows and tsm_system_time.
We will discuss those in greater detail in future blog posts.
Advantages
The premise of Big Data is that you must have detailed data to answer important business questions. But this is not always true, analysing trends and big changes is possible with statistically relevant sample of the data.
This is also true for exploratory research where TABLESAMPLE can help to quickly identify areas for further study.
When table sizes reach terabytes, getting statistically relevant output from the data is the main issue. No matter what optimizations you do, reading TBs of data off a disk will take time. With TABLESAMPLE, sampling is much easier and thanks to the extensibility, it’s possible to ensure the selected sample is relevant for the given use case.




Leave a Reply
Want to join the discussion?Feel free to contribute!