Random numbers

I’ve been slowly working on developing open source database systems performance testing tools from scratch.  One of the components of this toolset is a data generator that can build a dataset to be loaded into a database.  I’ll need a random number generator for that and these are the requirements that I think are most important:

• reproducible data
• fast

Being able to recreate the same data can be important when a particular set of data causes something interesting to happen.  Over the course of a test, data may change so I wanted to be able to start with the exact same set of data.  Another aspect to prepare for is when the data set is so large that it becomes impractical to save a copy of the raw data, much less a backup of the database.

Performance can be a significant time saver for large amounts of data.  If it takes 24 hours to generate 10 billion rows of data, a 20% speed improvement is almost 5 hours of time saved.  Whether that is in the form of algorithms used or programming language, the sum of many little improvements can turn into significant savings when days or more time is needed.  The 20% number is just an example so we need to evaluate what we can expect.

Next is narrowing down the random number generator to use.  More specifically, a pseudorandom number generator for two specific reasons: it is faster than using a true random number generator, and the results of a pseudorandom number generator are supposed to be reproducible.

I started with a few classes of pseudorandom number generators that were readily available in C (and Rust, but more on this another time) with a compatible license to the PostgreSQL license:

• Mersenne Twister
• permuted congruential generators
• shift-register generators

There are three properties I want to evaluate with these generators to see how they might impact my requirements:

1. How long does it take to generate numbers?
2. How long does it take to seed the generator?
3. Is it possible to advance the generator without having to generate numbers?

Equinix Metal provided hardware to the PostgreSQL Global Development Group allowing me to run some of these tests.  The system provided has a 48 core Intel(R) Xeon(R) CPU E5-2650 with 250GB of RAM.  The pseudorandom number generators aren’t going to stress the system too much by themselves, but we will hopefully see how a random data generator will perform at a later time.

The first test ran measures how fast 10 billion random numbers can be generated:

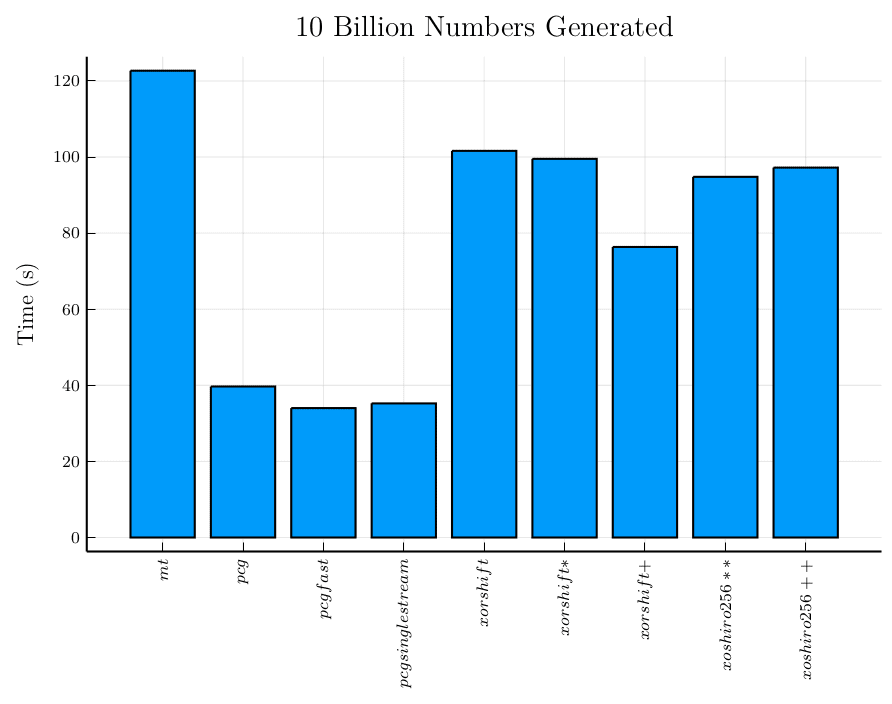
The permuted congruential generators are able to produce numbers more than twice as fast as any of the shift-register generators, and three times faster than the Mersenne Twister generator.  That looks like a good reason to continue experimenting with these generators to see how much impact that has on the overall performance of a random data generator.

Next let’s look at how expensive it is to seed a generator.  The reason for this is to determine how the random data generator can be constructed to produce consistent data.

One method to consider is to seed the generator per row of data in a table, so when parallelizing the data generator we know where to start the generator.

Another reason is because we might use a new generator for a particular column of data.  For example any column that needs a variable amount of numbers generated.  A Gaussian distribution uses a non deterministic number of random numbers in order to produce a result.  A random string uses a random number for the string length and one per character of the string.

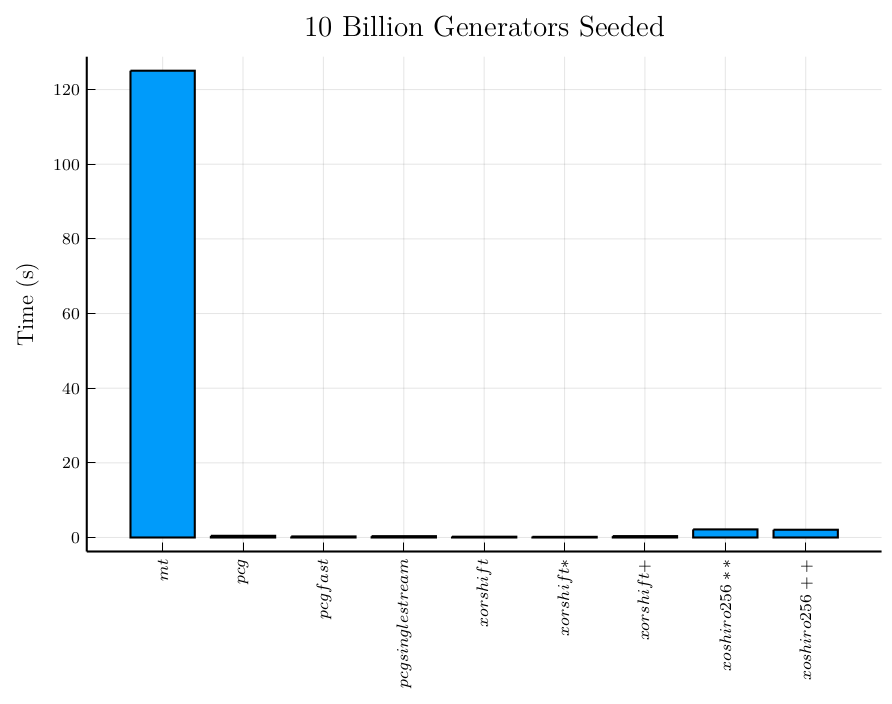
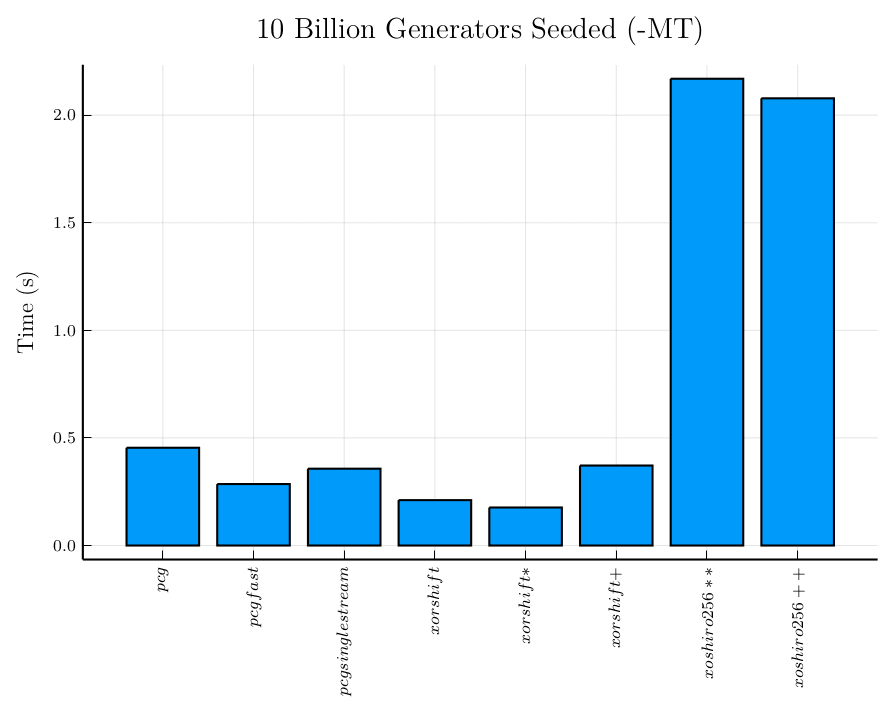
I present two charts, first including the Mersenne Twister generator, and then without.  Seeding the Mersenne Twister generator is two orders of magnitude slower than seeding any of the other generators so I wanted to get a better look at the others without the Mersenne Twister generator.  The shift-register generators vary a bit among themselves while the permuted congruential generators seem pretty more consistent and in the same order of magnitude as the faster shift-register generators.

Otherwise seeding the shift-register generators and permuted congruential generators both are an order or magnitude faster than their respective time to generate numbers.

The permuted congruential generators have the added functionality of advancing the generator to any point, which might help with parallelizing a data generator.

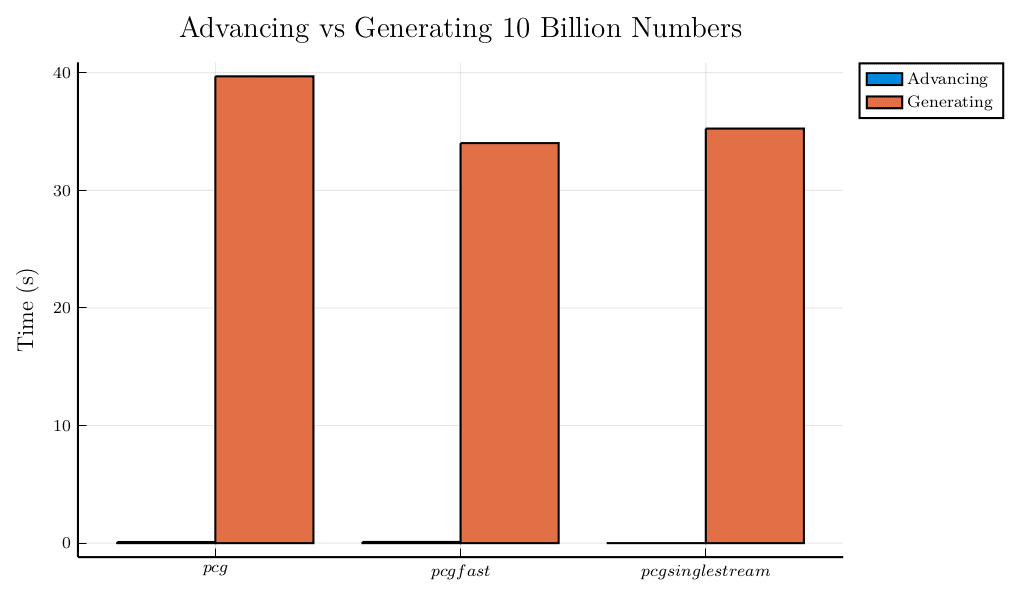
The function call to advance the generator 10 billion numbers as opposed to generating 10 billion numbers is a difference of a couple orders or magnitude in each case.

The results of these tests suggest to me that the permuted congruential generators have the best overall balance of performance between seeding, generating and parallelizing a data generator between these generators.  But the real test will be about what kind of impact these differences will really have in the data generator.